nLab Lie algebra object
Context
Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Categorical algebra
internalization and categorical algebra
-
algebra object (associative, Lie, …)
Contents
Idea
The notion of Lie algebra may be formulated internal to general linear monoidal categories (tensor categories). This general definition of Lie algebra objects internal to tensor categories subsumes variants of Lie algebras such as super Lie algebras.
Definition
As internal Lie algebras
Consider a commutative unital ring , and a (strict for simplicity) symmetric monoidal -linear category with braiding .
A Lie algebra object in is
-
an object
-
morphism (the Lie bracket)
such that the following conditions hold:
-
skew-symmetry:
Equivalently, in string diagram-notation in the ambient tensor category, the Lie action property looks as follows:
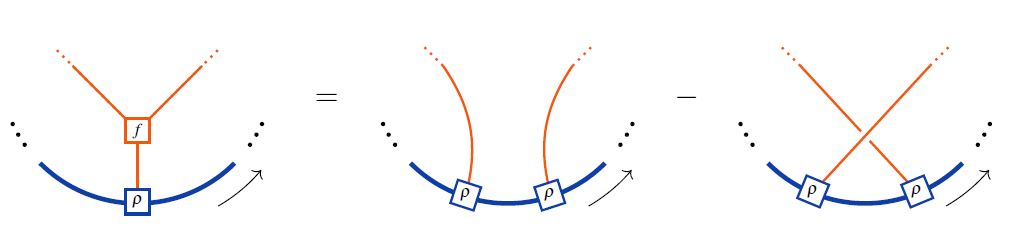
where the last line shows the equivalence to the Jacobi identity on the Lie algebra object itself in the case that the Lie action is the adjoint action.
graphics from Sati-Schreiber 19c
In the language of Jacobi diagrams this is called the STU-relation. and is the reason behind the existence of Lie algebra weight systems in knot theory. For more see also at metric Lie representation.
As algebras over the Lie operad
Equivalently, Lie algebra objects are the algebras over an operad over a certain quadratic operad, called the Lie operad, which is the Koszul dual of the commutative algebra operad.
Examples
Examples of types of Lie algebra objects:
-
If is the ring of integers and Mod = Ab is the category of abelian groups equipped with the tensor product of abelian groups, then a Lie algebra object is called a Lie ring.
-
If is a field and Vect is the category of vector spaces over equipped with the tensor product of vector spaces then a Lie algebra object is an ordinary Lie k-algebra.
-
If is a field and = sVect is the category of super vector spaces over , then a Lie algebra object is a super Lie algebra.
-
A Leibniz algebra is an internal Lie algebra in the Loday-Pirashvili category (Loday-Pirashvili 98)
-
Rozansky-Witten weight systems are Lie algebra weight systems for Lie algebra objects in the derived category of quasi-coherent sheaves (Roberts-Willerton 10)
Related concepts
References
General
(…)
Examples
For references on super Lie algebras see there.
On Leibniz algebras as Lie algebra objects in suitable tensor categories of linear maps:
- Jean-Louis Loday, Teimuraz Pirashvili, The tensor category of linear maps and Leibniz algebras, Georg. Math. J. vol. 5, n.3 (1998) 263–276 (doi:10.1023/B:GEOR.0000008125.26487.f3)
On Rozansky-Witten weight systems as Lie algebra weight systems for Lie algebra objects in the derived category of quasi-coherent sheaves, and unified Wheels theorem:
- Justin Roberts, Simon Willerton, On the Rozansky-Witten weight systems, Algebr. Geom. Topol. 10 (2010) 1455-1519 (arXiv:math/0602653)
Last revised on December 6, 2021 at 09:55:33. See the history of this page for a list of all contributions to it.